Hashing Table & Binary Tree

HASHING

---

Hashing adalah teknik yang digunakan untuk menyimpan dan mengambil key dengan cepat.

Dalam Hashing character string dapat ditransform menjadi sebuah nilai yang datanya pendek atau sebuah key yang mewakili string asli.

Hashing biasa digunakan untuk mengindeks dan mengambil item dalam data base karena lebih cepat menemukan item menggunakan hash key yang lebih pendek daripada menemukannya menggunakan nilai asli.

Hashing juga dapat didefinisikan sebagai konsep mendistribusikan key dalam array.

source: Powerpoint DataStructure Binus.

HASH TABLE

---

Hash Table adalah tabel (array) tempat dimana menyimpan string asli. Indeks tabel adalah Hashed Key sementara nilainya adalah string asli.

Ukuran table hash berbeda-beda biasanya beberapa urutan besarnya lebih rendah dari jumlah total string yang mungkin ada, sehingga beberapa string mungkin memiliki hash key yang sama.

sebagai contoh:

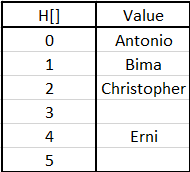
Misalkan kita ingin menyimpan 5 string: Antonio, Bima, Chirstopher, Erni ke tabel hash dengan ukuran 26. hash

Fungsi yang akan kita gunakan adalah "mengubah karakter pertama

setiap string menjadi angka antara 0..25 ”

(a akan menjadi 0, b akan menjadi 1, c akan menjadi 2, ..., z akan menjadi 25).

maka list mahasiswa tersebut dalam hash table akan terbuat seperti ini

HASH FUNCTION

---

Ada banyak cara untuk membuat sebuah Hash string menjadi sebuah key. Berikut ini adalah beberapa metode penting untuk membangun hash function

MID-Square

Mid-Square merupakan fungsi hashing dengan cara mengkuadratkan nilai string/indentifier yang kemudian digunakan dalam jumlah bit sesuai dengan tengah kotak untuk mendapatkan hash key.

Sebagai contoh

Nilai = 1003

Nilai 1003 dipangkatkan menjadi 1.006.009‬ nilai tersebut merupakan square value

Setelah itu ambil nilai tengah dari squre value yaitu 606 ini merupakan hasil dari Mid-Square Hashing.

Division

Division merupakan fungsi hashing dengan cara membagi nilai string/indentifier menggunakan operator modulus.

Sebagai contoh

Misalnya table menyimpan string. Fungsi hash yang sangat sederhana adalah menambahkan nilai ASCII dari semua karakter dalam string dan mengambil modulo ukuran tabel, misalnya 97.

Misalnya data "ABCD" maka ( 64+1 + 64+2 + 64+3 + 64+4) % 97 = 76 oleh karena itu data "ABCD" akan disimpan di 76.

Folding

Folding merupakan fungsi hashing dengan cara mempartisi string/indentifier menjadi beberapa bagian lalu ditambahkan bersama-sama untuk mendapatkan hash key

Sebagai contoh

Nilai = 1234

maka akan dipecah menjadi 2 part yaitu 12 dan 34

setelah itu ditambahkan 12+34 maka menjadi 46

maka hash keynya 46

Digit Extraction

Digit Extraction merupakan fungsi hashing dengan cara digit yang ditentukan sebelumnya dari nomor yang diberikan dianggap sebagai alamat hash.

Sebagai contoh

Nilai = 123456

jika kita hanya mengambil digit ke 1, 3 dan 5 maka kita akan mendapatkan

hash code = 135

Rotating Hash

Rotating Hash merupakan fungsi hashing dengan cara metode hash (seperti metode pembagian atau mid-square)

Setelah mendapatkan kode / alamat hash dari metode hash, lakukan rotasi.

Rotasi dilakukan dengan menggeser digit untuk mendapatkan alamat hash baru.

Sebagai contoh

diberikan hash address 12345

maka hasil dari rotating hashnya 54321

COLLISION

---

Collision terjadi jika kita ingin menyimpan string ini menggunakan fungsi hash sebelumnya (gunakan karakter pertama dari setiap string).

Cara untuk menyelesaikan collision ada 2 yaitu

1. Linear Probing

Cari slot kosong berikutnya dan letakkan string tersebut di sana.

2. Chaining

Masukkan string ke dalam slot sebagai chained list(linked list).

BASIC HASHING OPERATION

---

Search

Setiap kali suatu elemen harus dicari, hitung kode hash dari kunci yang dilewati dan temukan elemen tersebut menggunakan kode hash sebagai indeks dalam array. Gunakan linear probing untuk mendapatkan elemen di depan jika elemen tidak ditemukan pada kode hash yang dihitung.

deklarasi search

struct DataItem *search(int key) { //get the hash int hashIndex = hashCode(key); //move in array until an empty while(hashArray[hashIndex] != NULL) { if(hashArray[hashIndex]->key == key) return hashArray[hashIndex]; //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } return NULL; }

Insert

Setiap kali elemen dimasukkan, hitung kode hash dari kunci yang dilewati dan cari indeks menggunakan kode hash itu sebagai indeks dalam array. Gunakan linear probing untuk lokasi kosong, jika elemen ditemukan pada kode hash yang dihitung.

deklarasi insert

void insert(int key,int data) { struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem)); item->data = data; item->key = key; //get the hash int hashIndex = hashCode(key); //move in array until an empty or deleted cell while(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) { //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } hashArray[hashIndex] = item; }

Delete

Setiap kali elemen akan dihapus, hitung kode hash dari kunci yang dilewati dan cari indeks menggunakan kode hash itu sebagai indeks dalam array. Gunakan linear probing untuk mendapatkan elemen di depan jika elemen tidak ditemukan pada kode hash yang dihitung. Saat ditemukan, simpan item dummy di sana untuk menjaga kinerja tabel hash tetap utuh.

Deklarasi delete

struct DataItem* delete(struct DataItem* item) { int key = item->key; //get the hash int hashIndex = hashCode(key); //move in array until an empty while(hashArray[hashIndex] !=NULL) { if(hashArray[hashIndex]->key == key) { struct DataItem* temp = hashArray[hashIndex]; //assign a dummy item at deleted position hashArray[hashIndex] = dummyItem; return temp; } //go to next cell ++hashIndex; //wrap around the table hashIndex %= SIZE; } return NULL; }

source: https://www.tutorialspoint.com/data_structures_algorithms/hash_data_structure.htm

TREE & BINARY TREE

---

Tree adalah struktur data non-linear yang mewakili hubungan hierarkis di antara objek data.

Beberapa hubungan tree dapat diamati dalam struktur direktori atau hierarki organisasi.

Node di tree tidak perlu disimpan secara berdekatan dan dapat disimpan di mana saja dan dihubungkan oleh pointer.

TREE CONCEPT

---

DEGREE of TREE = 3

DEGREE of C = 2

HEIGHT = 3

PARENT of C = A

CHILDREN of A = B, C, D

SIBILING of F = G

ANCESTOR of F = A, C

DESCENDANT of C = F, G

Node di atas disebut sebagai root.

Garis yang menghubungkan induk ke anak adalah edge.

Node yang tidak memiliki anak disebut leaf.

Node yang memiliki parent yang sama disebut sibling.

Degree simpul adalah total sub pohon simpul.

height/depth adalah tingkat maksimum node dalam pohon.

Jika ada garis yang menghubungkan p ke q, maka p disebut ancestor q, dan q adalah decentdant dari p.

BINARY TREE CONCEPT

---

Binary tree adalah struktur data rooted tree di mana setiap node memiliki paling banyak dua anak.

Kedua anak itu biasanya dibedakan sebagai anak kiri dan anak kanan.

Node yang tidak memiliki anak disebut leaf.

Contoh binary tree dari 9 node, di-root simpul yang berisi 18.

Leaf adalah simpul yang mengandung 9, 12, 10 dan 23 karena tidak memiliki turunan.

TIPE-TIPE BINARY TREE

---

Perfect Binary Tree

PERFECT binary tree adalah binary tree di mana setiap level berada pada kedalaman yang sama.

Complete Binary Tree

Complete Binary Tree adalah binary tree di mana setiap level, kecuali mungkin yang terakhir, terisi penuh, dan semua node sejauh mungkin dibiarkan. Perfect Binary Tree adalah Complete Binary Tree.

Skewed Binary Tree

Skewed Binary Tree adalah binary tree di mana setiap node memiliki paling banyak satu anak.

Balanced Binary Tree

Balanced Binary Tree adalah binary tree di mana tidak ada daun yang jauh lebih jauh dari root daripada leaf lainnya (skema penyeimbangan yang berbeda memungkinkan definisi yang berbeda dari "jauh lebih jauh").

TRANSVERSAL

---

Ekspresi pada tree concept

struct tnode {

char chr;

struct tnode *left;

struct tnode *right; };

lalu buat ekspresi pada tree dari prefix

Bisa dideklarasikan dengan cara rekursif

char s[MAXN];

int p = 0;

void f(struct tnode *curr) {

if(is_operator(s[p])) {

p++; curr->left = newnode(s[p]);

f(curr->left);

p++; curr->right = newnode(s[p]);

f(curr->right);

} }

Prefix transversal

void prefix(struct tnode *curr){

printf( “%c “, curr->chr );

if ( curr->left != 0 ) prefix(curr->left);

if ( curr->right != 0 ) prefix(curr->right); }

Postfix transversal

void postfix(struct tnode *curr) {

if ( curr->left != 0 ) postfix(curr->left);

if ( curr->right != 0 ) postfix(curr->right); printf( “%c“, curr->chr );

}

Infix transversal

void infix(struct tnode *curr) {

if ( curr->left != 0 ) infix(curr->left);

printf( “%c“, curr->chr );

if ( curr->right != 0 ) infix(curr->right); }

Nama : Antonio Michael Kurniawan

NIM : 2301924063